In MMA winners keep winning and losers keep losing
23 Aug 2016In MMA, momentum is huge. Fighters who continue to extend their win streaks by dominating opponents can quickly work their way up the tables, awarding them the opportunity to fight tougher opponents, move to higher caliber fight organizations and maybe, ultimately win a title shot. On the flip side, it can be hard for fighters to recover from a loss; often a single loss is often a sign that a fighter’s confidence is shaken and their future performance will suffer.
In this post, I address one aspect of momentum in MMA: how a fighter’s performance in one fight affects their performance in their next fight. Summarizing the careers of over 150,000 fighters, I see that wins at any stage of a fighter’s career are an indicator of future success, while early losses are often enough to force a fighter to rethink their MMA dreams.
Each fighter’s career can be broken down into a simple sequence of wins and losses. For example, the career of Randy “the Natural” Couture can be summarized as: WWWWLLWWWLWWWLLWWLWLWLWWLLWWWL
To investigate how wins or losses impact future performance, instead of viewing Couture’s career in its entirety, we can investigate how a single win or loss impacts performance in the subsequent fight. To do this, I will make the simplifying assumption that careers are memoryless (a Markov process), so a fight’s result will only directly depend upon the fight immediately before it. For example, a fighter’s performance in their third fight ($n+1$) depends upon their second fight ($n$), but not on their first fight ($n-1$).
Adopting this convention, Randy Couture’s career can be described as a sequence of transitions: WW, WW, WW, WL, LL, LW, WW, WW, WL, LW, WW, WW, WL, LL, LW, WW, WL, LW, WL, LW, WL, LW, WW, WL, LL, LW, WW, WW, WL
Rather than just considering a fighter’s career as a sequence of wins and losses, we can also consider one other important milestone in each fighter’s career: their retirement. Couture hasn’t fought since 2011, so we can add one additional state to his career’s trajectory: his ultimate retirement. The final transition in his Markov chain will then be “LR”.
To identify trends in these trajectories, we can generate these Markov career trajectories for all fighters.
Processing fighter careers
The first step in building Markov career trajectories is to order each fighter’s fights by date, and reducing their career to a sequence of states: wins, losses and if they are not active, retirement (for our purposes, no wins/losses in the last 14 months).
ordered_fights <- fights %>%
# only look at fighters, the fight result and fight date
select(Fighter_link, Result, Date) %>%
# only look at fights ending in a win or loss (~98%)
filter(Result %in% c("win", "loss"),
# look at fights with a valid date
!is.na(Date)) %>%
# for each fighter chronologically order bouts
group_by(Fighter_link) %>%
arrange(Date) %>%
mutate(Fight_number = 1:n())
# find the most recent date in the dataset
most_recent_fight <- max(ordered_fights$Date, na.rm = T)
retirement_cutoff <- 1.2 # years
fighter_retirement <- ordered_fights %>%
# only look at the most recent fight of each fighter
slice(n()) %>%
ungroup %>%
# determined whether this date suggests the fighter retired
# calculate time between most recent fight in dataset and each fighters most recent fight
mutate(time_since_most_recent_fight = difftime(most_recent_fight, Date, units = "days")) %>%
# determine whether this elapsed time is over the retirement cutoff
mutate(is_retired = ifelse(time_since_most_recent_fight > 365*retirement_cutoff, T, F)) %>%
filter(is_retired) %>%
# add an additional state to the fight sequence indicating that
# each fighter retired after their last fight
mutate(Result = "retired",
Fight_number = Fight_number + 1) %>%
select(Fighter_link:Fight_number)
ordered_fights <- bind_rows(ordered_fights, fighter_retirement) %>%
group_by(Fighter_link) %>%
arrange(Fight_number) %>%
select(-Date)
kable(ordered_fights %>% arrange(Fighter_link, Fight_number) %>% ungroup %>% slice(1000:1008))| Fighter_link | Result | Fight_number |
|---|---|---|
| /fighter/Aaron-Harris-60857 | retired | 3 |
| /fighter/Aaron-Harrison-87433 | win | 1 |
| /fighter/Aaron-Harrison-87433 | retired | 2 |
| /fighter/Aaron-Hart-60266 | win | 1 |
| /fighter/Aaron-Hart-60266 | loss | 2 |
| /fighter/Aaron-Hart-60266 | retired | 3 |
| /fighter/Aaron-Hartman-39354 | loss | 1 |
| /fighter/Aaron-Hartman-39354 | win | 2 |
| /fighter/Aaron-Hartman-39354 | win | 3 |
Considering fights as a markov process
With each fighter represented as a sequence of wins and losses, possibly ending in retirement, we can reduce these careers into a sequence of Markov chain transitions. This can be easily performed using an inner join of fight# and fight#-1 for each fighter.
# pair adjacent results in a fighters career
state_pairs <- ordered_fights %>%
# define the "from" states
select(Fighter_link, from_state = Result, from = Fight_number) %>%
inner_join(
# define the "to" states
# match "from" and "to" where fighters match and to = from + 1
ordered_fights %>%
select(Fighter_link, to_state = Result, to = Fight_number) %>%
mutate(from = to-1), by = c("Fighter_link", "from"))
kable(head(state_pairs %>% ungroup %>% select(from, from_state, to, to_state), 8))| from | from_state | to | to_state |
|---|---|---|---|
| 1 | win | 2 | retired |
| 1 | loss | 2 | retired |
| 1 | win | 2 | win |
| 1 | loss | 2 | loss |
| 1 | win | 2 | loss |
| 1 | loss | 2 | retired |
| 1 | loss | 2 | retired |
| 1 | win | 2 | win |
Patterns such as how frequently wins are followed by losses cannot be accurately tested for most fighters because the average career length of fighters is very short. To circumvent this limitation, we can assume that the identity of individual fighters is not important and we are just interested in sequences of win-loss-retirement transitions. Having ignored individuals, we can pool sequences, for instance, to test how frequently wins are followed by wins, losses or retirement, and how these transitions change with how many fights have elapsed. Even with this pooling, we will still not have much data at very high fight numbers, like the transition between fight 100 to fight 101. When looking at these larger fight numbers, some pooling is done for visualization and to improve accuracy. Interestingly, extremely high fight numbers are almost solely informed by a single fighter, Travis Fulton (the pathological “Fulton zone”). Travis Fulton has had more than 300 professional fights, almost 170 fights more than the second most prolific fighter Shannon Ritch.
# group some intervals of fights together to allow for better estimation
sequence_labels <- data.frame(fight_n = 1:max(state_pairs$to)) %>%
mutate(label = as.character(fight_n))
sequence_labels$label[11:30] <- rep(paste(seq(11, 29, 2), seq(12, 30, 2), sep = "-"), each = 2)
sequence_labels$label[31:70] <- rep(paste(seq(31, 66, 5), seq(35, 70, 5), sep = "-"), each = 5)
sequence_labels$label[sequence_labels$fight_n > 70] <- ">70"
sequence_labels <- sequence_labels %>%
mutate(label = factor(label, levels = unique(sequence_labels$label)))
# seperate interval into win, loss and retired states
all_label_levels <- expand.grid(fight_n = c(levels(sequence_labels$label), "boundary"),
state = c("win", "loss", "retired")) %>%
mutate(label = paste(fight_n, state, sep = "-")) %>%
filter(!(fight_n == 1 & state == "retired"))
# summarize fighters states and transitions using new groupings
state_pairs <- state_pairs %>%
# count the from result, the to result and what fight number it is for
ungroup %>%
count(from_state, to_state, from) %>%
# add the aggregated labels for fight numbers
left_join(sequence_labels, by = c("from" = "fight_n")) %>%
# recount with new labels
dplyr::count(from_state, to_state, label, wt = n) %>%
ungroup %>%
arrange(label)
# normalize counts to find transition probabilities
state_pairs <- state_pairs %>%
group_by(label) %>%
mutate(transition_Pr = nn/sum(nn)) %>%
mutate(from_label = paste(label, from_state, sep = "-"),
to_label = paste(c(levels(label), "boundary")[as.numeric(label)+1], to_state, sep = "-")) %>%
mutate(from_label = factor(from_label, levels = all_label_levels$label),
to_label = factor(to_label, levels = all_label_levels$label))
kable(head(state_pairs, 10))| from_state | to_state | label | nn | transition_Pr | from_label | to_label |
|---|---|---|---|---|---|---|
| loss | loss | 1 | 19215 | 0.1450265 | 1-loss | 2-loss |
| loss | retired | 1 | 43010 | 0.3246209 | 1-loss | 2-retired |
| loss | win | 1 | 14082 | 0.1062849 | 1-loss | 2-win |
| win | loss | 1 | 15791 | 0.1191837 | 1-win | 2-loss |
| win | retired | 1 | 18792 | 0.1418339 | 1-win | 2-retired |
| win | win | 1 | 21603 | 0.1630501 | 1-win | 2-win |
| loss | loss | 2 | 11002 | 0.1660579 | 2-loss | 3-loss |
| loss | retired | 2 | 12889 | 0.1945392 | 2-loss | 3-retired |
| loss | win | 2 | 8634 | 0.1303167 | 2-loss | 3-win |
| win | loss | 2 | 10931 | 0.1649863 | 2-win | 3-loss |
Visualizing transitions between wins and losses across fighter’s careers
Now that we have summarized how frequently wins and losses are followed by either a win, loss, or retirement at the different stages of fighters’ careers, we want to generate some informative summaries. To summarize these transitions, I will present three alternative visualizations that highlight different features of the data.
Conditional transition probabilities
To determine how the result of one fight (win or loss) affects the next fight (win, loss, or retirement), we can use conditional probabilities, for example how often a fighter wins given that they won their previous fight. Because we are also interested in how the trajectories of a fighter’s career change with experience, we want to visualize how these transition probabilities might change with a fighter’s number of fights.
library(ggplot2)
path_theme <- theme(
text = element_text(size = 20, color = "black"),
axis.text = element_text(color = "black"),
axis.text.x = element_text(angle = 60, hjust = 1),
axis.title = element_text(color = "black", size = 25),
axis.ticks = element_line(size = 0.5, color = "black"),
axis.ticks.length = unit(0.2, "cm"),
panel.grid.major.x = element_blank(),
panel.grid.minor = element_blank(),
panel.grid.major.y = element_line(size = 0.5, color = "white"),
panel.background = element_rect(fill = "gray90"),
legend.position = "none")
# look at all transitions between win, loss and retirement
state_pairs_all_transitions <- state_pairs %>%
group_by(from_label) %>%
mutate(transition_Pr = transition_Pr/sum(transition_Pr),
from_to_state = paste0(from_state, "->", to_state))
all_transition_plot <- ggplot(state_pairs_all_transitions,
aes(x = label, y = transition_Pr, color = from_state,
fill = from_state, linetype = to_state, group = from_to_state,
shape = from_to_state)) +
geom_point(size = 4) +
geom_smooth(method = "loess") +
geom_label(data = state_pairs_all_transitions %>% filter(label == "29-30"),
aes(label = from_to_state, transition_Pr = transition_Pr+0.05),
alpha = 0.5, color = "black", size = 10) +
scale_x_discrete("Number of fights") +
scale_y_continuous("Transition probability", expand = c(0,0)) +
scale_fill_brewer(palette = "Set2") + scale_color_brewer(palette = "Set2") +
path_theme +
ggtitle("Transitions between win, loss and retired")
# hide retirement
state_pairs_win_loss_transitions <- state_pairs %>%
filter(to_state != "retired") %>%
group_by(from_label) %>%
mutate(transition_Pr = transition_Pr/sum(transition_Pr),
from_to_state = paste0(from_state, "->", to_state))
no_retirement_plot <- ggplot(state_pairs_win_loss_transitions,
aes(x = label, y = transition_Pr, color = from_state,
fill = from_state, linetype = to_state, group = from_to_state,
shape = from_to_state)) +
geom_point(size = 4) +
geom_smooth(method = "loess") +
geom_label(data = state_pairs_win_loss_transitions %>% filter(label == "29-30"),
aes(label = from_to_state, transition_Pr = transition_Pr+0.05),
alpha = 0.5, color = "black", size = 10) +
scale_x_discrete("Number of fights") +
scale_y_continuous("Transition probability", expand = c(0,0)) +
scale_fill_brewer(palette = "Set2") + scale_color_brewer(palette = "Set2") +
path_theme +
ggtitle("Excluding retirement")
suppressPackageStartupMessages(library(gridExtra))
grid.arrange(all_transition_plot, no_retirement_plot, ncol = 2)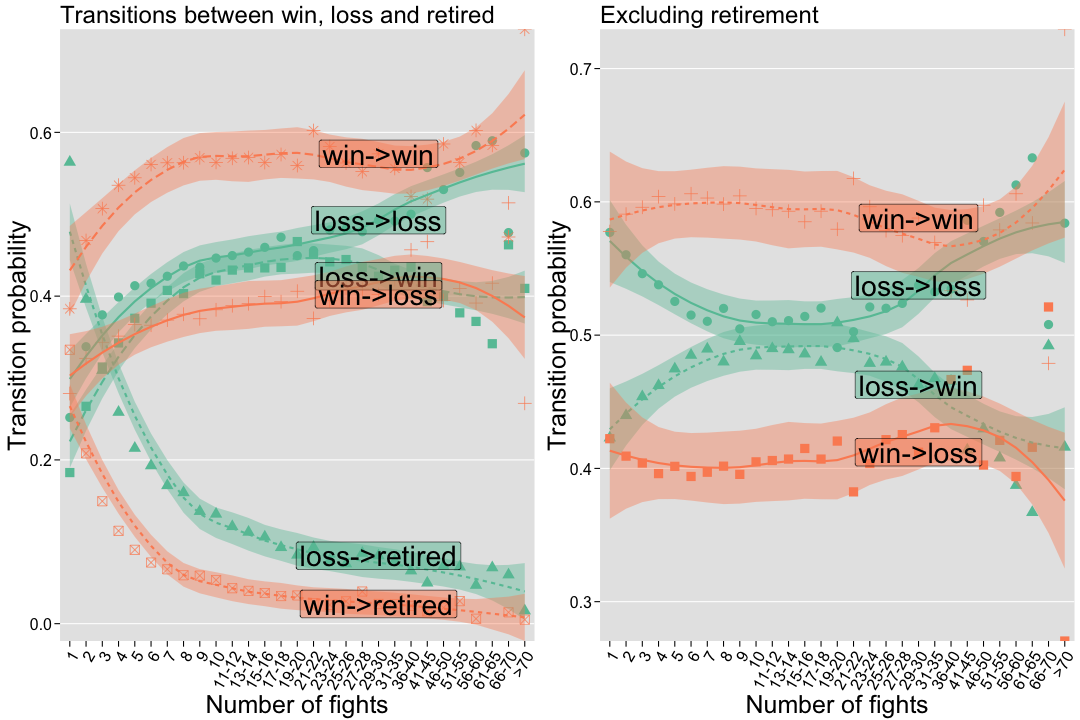
This fitted scatter plot reveals several important aspects of win-loss transitions:
- If a winning fighter keeps fighting, they are likely to keep winning regardless of where they are in their career (~60% chance).
- If either a very junior (<5 fights) or extremely experienced fighter (>30 fights) loses a bout, they are likely to keep losing; however, fighters with intermediate experience are more likely to rebound from a loss.
- Fighters are very likely to retire within their first few fights; the chance of retirement decreases quickly with experience, and fighters are much more likely to retire after a loss than after a win.
Transitions on a network
In order to estimate transition probabilities, I assumed that MMA career results could be represented as a Markov process, whereby a fighter’s behavior in a future fight could be fully described by their previous fight’s outcome. From the previous plot, it is not clear that I am describing fights as transitions between distinct states. To convey this point, the quantitative data from the above plot can be projected onto a network diagram generated using igraph and ggraph.
# individual states
state_summary <- state_pairs %>%
ungroup %>%
count(from_label, wt = nn) %>%
rename(label = from_label)
state_summary <- all_label_levels %>%
mutate(label = factor(label, levels = label)) %>%
left_join(state_summary, by = "label") %>%
mutate(x = as.numeric(fight_n),
y = ifelse(state == "win", 3, as.numeric(NA)),
y = ifelse(state == "loss", 2, y),
y = ifelse(state == "retired", 1, y)) %>%
select(label, state, n, x, y)
# wrap states in a big circle
inner_d = 2
slack_pos = 5
total_pos = diff(range(state_summary$x)) + slack_pos
state_summary <- state_summary %>%
mutate(theta = pi + (2*pi/total_pos)*(x + (slack_pos-1)/2)) %>%
mutate(t_x = cos(theta)*(y + inner_d),
t_y = sin(theta)*(y + inner_d)) %>%
mutate(node_label = toupper(substr(state, 1, 1))) %>%
mutate(display = ifelse(grepl('^boundary', label), F, T))
# generate labels for fight#
fight_n_labels <- all_label_levels %>% filter(state == "win") %>%
mutate(x = as.numeric(fight_n),
y = 3.5) %>%
mutate(theta = pi + (2*pi/total_pos)*(x + (slack_pos-1)/2)) %>%
mutate(t_x = cos(theta)*(y + inner_d),
t_y = sin(theta)*(y + inner_d)) %>%
filter(fight_n != "boundary")
# transitions between states
state_transitions <- state_pairs %>%
ungroup %>%
group_by(from_label) %>%
mutate(transition_Pr = transition_Pr/sum(transition_Pr)) %>%
select(from_label, to_label, nn, transition_Pr)
suppressPackageStartupMessages(library(igraph))
library(ggraph)
career_transitions <- graph_from_data_frame(state_transitions, vertices = state_summary)
graph_theme <- theme_minimal() +
theme(axis.text = element_blank(), panel.grid = element_blank(),
axis.title = element_blank(), legend.key.size = unit(0.5, "inches"),
legend.text = element_text(size = 25), legend.title = element_text(size = 25),
plot.background = element_rect(fill = "white", color = "white"), text = element_text(color = "black"))
ggraph(career_transitions, "manual", node.positions = state_summary %>% select(x = t_x,y = t_y)) +
geom_edge_link(aes(width = transition_Pr*3, color = transition_Pr), arrow = arrow()) +
geom_node_point(aes(x = x, y = y, alpha = ifelse(display, 1, 0)), size = 10) +
geom_node_text(aes(x = x, y = y, label = node_label, alpha = ifelse(display, 1, 0)), color = "white") +
scale_alpha_identity() +
scale_edge_width_identity() +
scale_edge_color_gradientn("Pr(transition)", colours = c("dodgerblue4", "dodgerblue1", "gray70", "firebrick1", "firebrick4"), limits = c(0,1)) +
#scale_edge_color_gradientn(colours = c("deepskyblue", "blue", "black", "firebrick1", "red"), limits = c(0,1)) +
graph_theme +
geom_text(data = fight_n_labels, aes(x = t_x, y = t_y, label = fight_n), size = 5)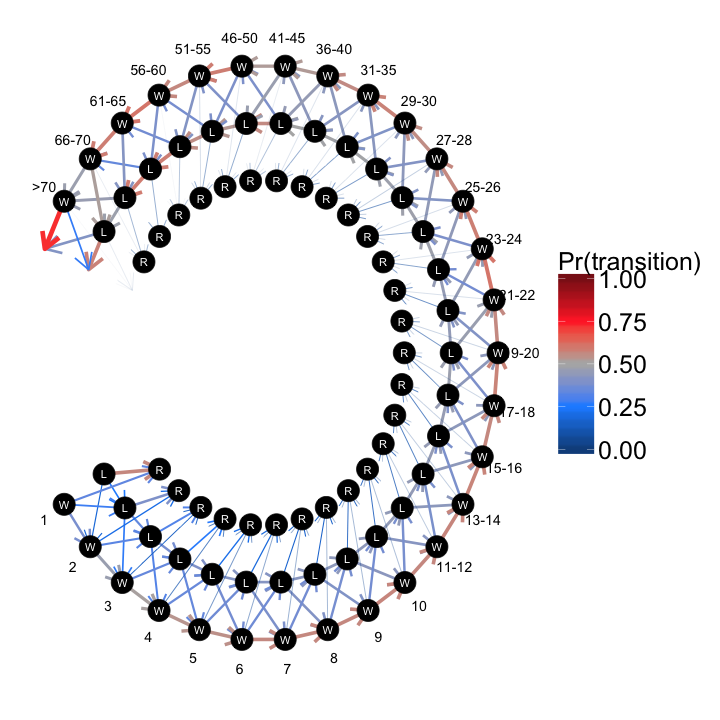
This network-based plot conveys the nature of the full analysis while containing the same data as the scatter plot. (The exact transition probabilities are more clear in the scatter plot, however.) This network visualization suggests that at most experience levels, there are effectively two tracks: wins lead to further wins, and losses lead to further losses, while transitions between these two tracks are less frequent.
Sankey plot
While the two previous plots effectively summarize the state and transitions of a fighter’s career, they do not convey one important aspect of these states; the frequency of the states. As shown above, most fighters are likely to retire quickly following an early loss, or even a win. Using a Sankey plot (available using the googleVis package), we can convey both the transitions between and the frequency of states.
suppressMessages(suppressPackageStartupMessages(library(googleVis)))
sankey_format <- state_pairs %>%
filter(as.numeric(label) < 20) %>%
filter(to_state != "retired") %>% ungroup %>%
select(from_label, to_label, counts = nn)
Sankey <- gvisSankey(sankey_format,
from="from_label", to="to_label", weight="counts",
options = list(width = 800, height = 500))
suppressMessages(plot(Sankey))
print(Sankey, tag="chart")While the Sankey plot captures the two-track nature of the network plot, it more clearly conveys the role of retirement in shaping the pool of fighters. Since the only states represented in this plot are wins and losses, when a win or loss is followed by retirement the plot will just trail off. Thus, as we progress left-to-right on this plot from junior fighters to experienced fighters, we see a massive increase in white space that reflects the washout of fighters before reaching this milestone.
Summary
Using a Markov modeling approach, I was able to reveal some interesting aspects of MMA fighters’ careers. Generally, winners keep on winning and losers keep on losing, or they quickly retire. This two track nature of MMA careers suggests that either a fighter carries momentum into their next match (for better or worse) or that many MMA fights are mismatched such that fighters reliably win or lose repeatedly. By applying the Markov assumption we cannot discriminate between the role of momentum and mismatches; however in my next post, I will evaluate the relative influence of these factors.