MMA styles I: grouping finishes using large-scale data
29 Sep 2016MMA fighters use a mixture of martial arts and the way that they win fights reflects their personal style.
A useful way of understanding the styles of fighters is if we (1) determine the styles of individual fighters and, (2) understand the set of techniques that an individual style entails. To investigate the latter question, rather than assuming that the grouping of techniques was known (such as heel hooks and triangle chokes contributing to a BJJ game), I determined whether such groupings could naturally emerge based on how frequently finishes have been used by the same fighters (i.e. do fighters who win with armbars tend to win with triangle chokes?)
Using data from ~120,000 wins across 35,000 fighters, I determined how frequently each pair of 50 common finishes was used by the same fighters relative to chance, allowing me to identify ~300 pairs of finishes that are commonly used together by fighters. These finish pairs can be used to more broadly organize finishes, grouping finishes that share similar partners.
Importing fight data
I only used fighters who had multiple finishes so that I could determine how those shared finishes were related. I filtered fighters with less than two finishes as well as fights where the finishes are not well recorded. The only information required for this analysis was a list of fighters and a summation of how they won all of their fights.
suppressPackageStartupMessages(library(dplyr))
fight_threshold <- 2 # fighters with N >= fight_threshold well-formed fights will be analyzed
# load all_bouts
data(all_bouts)
# filter results with either vague finishes (e.g. KO) or inconsistent record (e.g. won by draw)
overall_results <- all_bouts %>%
filter(!is_inconsistent & !is_vague) %>%
# filter fighters with greater than 2 wins (fight_threshold)
group_by(Fighter_link) %>%
filter(sum(Result == "win") >= fight_threshold) %>%
# save a unique fighter indicator and each win finish
filter(Result == "win") %>%
select(Fighter_link, Finish = Overall_finish)
# pull out general categories as well (primarily for labelling) and a category color
general_finishes <- all_bouts %>%
dplyr::filter(Result == "win") %>%
dplyr::select(Finish = Overall_finish, General_Finish = General_finish) %>%
unique()
general_finishes <- general_finishes %>%
left_join(
general_finishes %>%
dplyr::select(General_Finish) %>%
unique() %>%
mutate(color = RColorBrewer::brewer.pal(length(General_Finish),"Set2")),
by = "General_Finish")
kable(head(overall_results, 8))| Fighter_link | Finish |
|---|---|
| /fighter/Andrei-Arlovski-270 | Unanimous Decision |
| /fighter/Andrei-Arlovski-270 | Punches (TKO) |
| /fighter/Andrei-Arlovski-270 | Punches (KO) |
| /fighter/Andrei-Arlovski-270 | Split Decision |
| /fighter/Andrei-Arlovski-270 | Punches (TKO) |
| /fighter/Andrei-Arlovski-270 | Unanimous Decision |
| /fighter/Andrei-Arlovski-270 | Unanimous Decision |
| /fighter/Andrei-Arlovski-270 | Punches (TKO) |
Shown in the table “overall_results,” there are 37843 fighters who have won fights using a total of 50 distinctive finishes. There are total of 188566 wins represented.
Determining similar usage of finishes
To identify finishes that cooccur frequently, I will first show how to determine how many times each pair of finishes (such as armbars and punches) has been used by a single fighter. I will then expand the results from a single fighter to cover all fighters. This will reveal how many times pairs of finishes have been used together by the same fighters. Because some finishes occur more frequently (such as armbars and rear-naked chokes) than others (such as gogoplatas and flying knees), this observed frequency of cooccurrence must be compared to an expectation if all finishes were used randomly. This relative shared finish frequency (RSFF) will ultimately tell us how pairs of finishes are linked and significance testing will tell us whether this enrichment is to be expected.
Looking at a single fighter
To determine how many times each pair of finishes has been used across all fighters, I will first consider a single hypothetical fighter. Let’s assume that this fighter has won 6 fights: 3 by armbar, 2 by punches and 1 by a rear-naked choke (RNC). A nuance here is that the fighter has won by armbar and punches multiple times. For this fighter, multiple armbars cooccur more often than multiple RNCs and armbars cooccur with punches more frequently than with RNCs. In order to appropriately analyze this dataset, our notion of finish cooccurrence must reflect this clear intuition.
To analyze cooccurrence, I view each win as a separate entry; our fighters’ wins can be represented as \([A1, A2, A3, P1, P2, R1]\). I then determined how many linkages there are within wins of the same finish (for instance between armbars) as well as between finishes (for instance between armbars and punches).
Looking at the repeated cooccurrence of armbars (\([A1, A2, A3]\)), the unique pairs of these finishes are \([A1, A2]\), \([A1, A3]\) and \([A2, A3]\). More generally, the number of links between the \(n\) instances of the same finish is \({n \choose 2}\).
Looking at cooccurrence of pairs of different finishes, as an example, I will consider the cooccurrence of armbars (\([A1, A2, A3]\)) and punches (\([P1, P2]\)). The unique pairs of these finishes are \([A1, P1]\), \([A1, P2]\), \([A2, P1]\), \([A2, P2]\), \([A3, P1]\) and \([A3, P2]\). For any pair of \(n\) finishes of one type and \(m\) of another, the total number of pairs is \(nm\).
For the three unique submissions above, all pairs of edges are:

As noted above, the associations between multiple armbars are stronger than those between multiple RNCs, and the association between armbars and punches is stronger than that between armbars and RNCs.
Looking across all fighters
When scaling to all fighters, I essentially needed to carry out the same calculations on each fighter and then add the links across all fighters. This will yield a 50 x 50 matrix including the cooccurrence of all finishes across all fighters. Diagonal elements of this matrix \(\mathbf{E}\) will be cooccurrence of the same finish for fighters, while off-diagonal elements are linkages across distinct finishes.
A shortcut to this calculation can be found using matrix multiplication, treating diagonal and off-diagonal elements separately.
Each off-diagonal element that represents counts of two finishes \(j\) and \(k\) of a fighter \(i\) can be found as: \(e_{kj} = \sum_{i = 1}^{37843}f_{ij}f_{ik}\). (\(\mathbf{F}\) is a matrix where each row represents a fighter and each column is counts of a finish.) This is equivalent to:
\[\text{off-diag}(\mathbf{E}) = \text{off-diag}(\mathbf{F}\mathbf{F}^{T})\]Each diagonal element that represents cooccurrence of the same type of finish \(j\) in a fighter \(i\) can be found as: \(e_{jj} = \sum_{i = 1}^{37843}{f_{ij} \choose 2}\). This is equivalent to (where \(n \ge 1\)):
\[\text{diag}(\mathbf{E}) = \text{diag}((\mathbf{F}-1)\mathbf{F}^{T}/2)\]\(\mathbf{E}\) is symmetric across the diagonal due to duplication of entries (i.e. counts of armbar-triangle = triangle-armbar). To avoid this double counting of some entries, I only consider the upper triangular matrix of \(\mathbf{E}\) This is done by setting all elements below the diagonal to zero.
In order to determine whether the finishes in \(\mathbf{E}\) are higher for some pairs than could be expected by chance, I determined the expected counts of \(\mathbf{E}\) assuming independence of finishes. The frequency of a single finish \(j\) in \(\mathbf{E}\) can be found by summing each row \(j\) and column \(j\) of \(\mathbf{E}\). If \(j = n\) we are double counting a finish since it is both elements of a pair.
\[v_{j} = \sum_{n = 1}^{50}e_{jn} + e_{nj}\]Before comparing pairs of finishes (\(\mathbf{E}\)) and counts of single linked finishes (\(\mathbf{v}\)), it is useful to express these as probabilities rather than as counts. This involves dividing counts of individual classes by the sum of all counts.
\[\text{Pr}(e_{jk}) = \frac{e_{ij}}{\sum\mathbf{E}}\] \[\text{Pr}(v_{j}) = \frac{v_{j}}{\sum\mathbf{v}}\]If two finishes \(v_{j}\) and \(v_{k}\) are independent, the probability of picking both of them is equal to the product of their individual probabilities. If \(j \neq k\), then I could also either first pick finish \(j\) and then \(k\) or first pick \(k\) and then \(j\).
\[e^{\text{independent}}_{jk} = 2v_{j}v_{k}\] \[e^{\text{independent}}_{jj} = v_{j}^{2}\]The ratio of the observed probability of finish cooccurrence \(\mathbf{E}\) to the expected cooccurrence \(\mathbf{E}^{independent}\) indicates how relatively likely (high value) or unlikely (low value) pairs of finishes are to cooccur.
To calculate this relative shared finish frequency (RSFF), I implemented the above approach as a function using matrix algebra. Using a function, I can cleanly calculate RSFF many times (this will be important later), and the speed-up using matrix algebra makes the calculation fast (~1 second to crunch the whole dataset).
RSFF_calculate <- function(results){
# generate a matrix with fighters as rows, finishes as columns and entries as win counts
finish_contingency <- results %>%
count(Fighter_link, Finish) %>%
tidyr::spread(Finish, n, fill = 0)
finish_contingency_matrix <- finish_contingency %>%
ungroup() %>%
select(-Fighter_link) %>%
as.matrix()
rownames(finish_contingency_matrix) <- finish_contingency$Fighter_link
# off-diagonal cooccurrences sum(n choose 1 * m choose 1) = sum(nm)
offdiag_inner <- t(finish_contingency_matrix) %*% finish_contingency_matrix
# diagonal elements: sum(n choose 2)^2 = sum(n * (n-1))/2
diag_contingency_matrix_minusone <- finish_contingency_matrix - 1
diag_contingency_matrix_minusone[diag_contingency_matrix_minusone < 0] <- 0
diag_inner <- (t(finish_contingency_matrix) %*% diag_contingency_matrix_minusone)/2
# combine diagonal and off-diagonal to generate an overall adjacent matrix
total_pairs <- offdiag_inner
diag(total_pairs) <- diag(diag_inner)
total_pairs[lower.tri(total_pairs)] <- NA
# count number of times each finish is in a pair (count pairs between the same finish twice)
Pr_finish <- (rowSums(total_pairs, na.rm = T) + colSums(total_pairs, na.rm = T))/2
Pr_finish <- data.frame(Finish = names(Pr_finish), Pr_Finish = unname(Pr_finish)/sum(Pr_finish), stringsAsFactors = F)
total_pair_df <- total_pairs %>%
as.data.frame() %>%
mutate(Finish_from = rownames(.)) %>%
tidyr::gather("Finish_to", "Edge_count", -Finish_from, convert = T) %>%
tbl_df() %>%
filter(!is.na(Edge_count)) %>%
mutate(Pr_Edge = Edge_count/sum(Edge_count)) %>% # normalize edge_count to one
left_join(Pr_finish %>%
select(Finish_from = Finish, from_Pr = Pr_Finish), by = "Finish_from") %>%
left_join(Pr_finish %>%
select(Finish_to = Finish, to_Pr = Pr_Finish), by = "Finish_to") %>%
# if finish1 = finish2: Pr(link) = p^2
# if finish1 != finish2: Pr(link) = 2pq
mutate(expected_Pr_Edge = ifelse(Finish_from == Finish_to, from_Pr^2, 2*from_Pr*to_Pr),
RSFF = Pr_Edge/expected_Pr_Edge)
total_pair_df
}
RSFF_observed <- RSFF_calculate(overall_results)
kable(head(RSFF_observed %>% dplyr::select(-from_Pr, -to_Pr), 8))| Finish_from | Finish_to | Edge_count | Pr_Edge | expected_Pr_Edge | RSFF |
|---|---|---|---|---|---|
| Americana | Americana | 1 | 0.0000012 | 0.0000000 | 37.6734499 |
| Americana | Anaconda Choke | 0 | 0.0000000 | 0.0000012 | 0.0000000 |
| Anaconda Choke | Anaconda Choke | 276 | 0.0003413 | 0.0000106 | 32.0678720 |
| Americana | Ankle Lock | 2 | 0.0000025 | 0.0000017 | 1.4355990 |
| Anaconda Choke | Ankle Lock | 4 | 0.0000049 | 0.0000310 | 0.1594505 |
| Ankle Lock | Ankle Lock | 247 | 0.0003055 | 0.0000226 | 13.5122560 |
| Americana | Arm-Triangle Choke | 6 | 0.0000074 | 0.0000060 | 1.2452511 |
| Anaconda Choke | Arm-Triangle Choke | 243 | 0.0003005 | 0.0001073 | 2.8007529 |
Visualizing finish similarity
One interesting facet of this analysis is that I am not only interested in single pairs of finishes that are likely to cooccur, but also expect that sets of finishes (such as all leg locks or different types of kicks) may cooccur as a group. In the 50 x 50 summary of RSFF, this group structure would manifest as block diagonal structure if the finishes were appropriately ordered. To determine this ordering of finishes, I used hierarchical clustering and then visualized the resulting reordered matrix with a heatmap.
suppressPackageStartupMessages(library(gplots))
library(colorRamps)
# make a heatmap of relative shared finish frequency (RSFF)
RSFF_matrix <- RSFF_observed %>%
filter(Edge_count >= 2) %>%
mutate(log_RSFF = log2(RSFF)) %>%
select(Finish_from, Finish_to, log_RSFF)
RSFF_matrix <- rbind(RSFF_matrix,
# add the other diagonal of matrix
RSFF_matrix %>% select(Finish_from = Finish_to, Finish_to = Finish_from, log_RSFF) %>%
filter(Finish_from != Finish_to)) %>%
tidyr::spread(key = Finish_to, value = log_RSFF) %>%
as.data.frame()
rownames(RSFF_matrix) <- RSFF_matrix$Finish_from
RSFF_matrix <- RSFF_matrix[,colnames(RSFF_matrix) != 'Finish_from']
RSFF_matrix <- as.matrix(RSFF_matrix)
# threshold
RSFF_matrix[RSFF_matrix > 3] <- 3
RSFF_matrix[RSFF_matrix < -3] <- -3
heatmap.side.colors <- data.frame(Finish = colnames(RSFF_matrix), stringsAsFactors = F) %>%
left_join(general_finishes, by = "Finish")
hclust_ward <- function(x){hclust(x, method = "ward.D2")}
par(mar=c(3,3,4,10)+0.1)
heatmap.2(RSFF_matrix, trace = "none", symm = T, col = blue2yellow(100), hclustfun = hclust_ward,
ColSideColors = heatmap.side.colors$color, RowSideColors = heatmap.side.colors$color,
cexRow = 1.3, cexCol = 1.3, margins =c(12,12), key.title = "log2(RSFF)")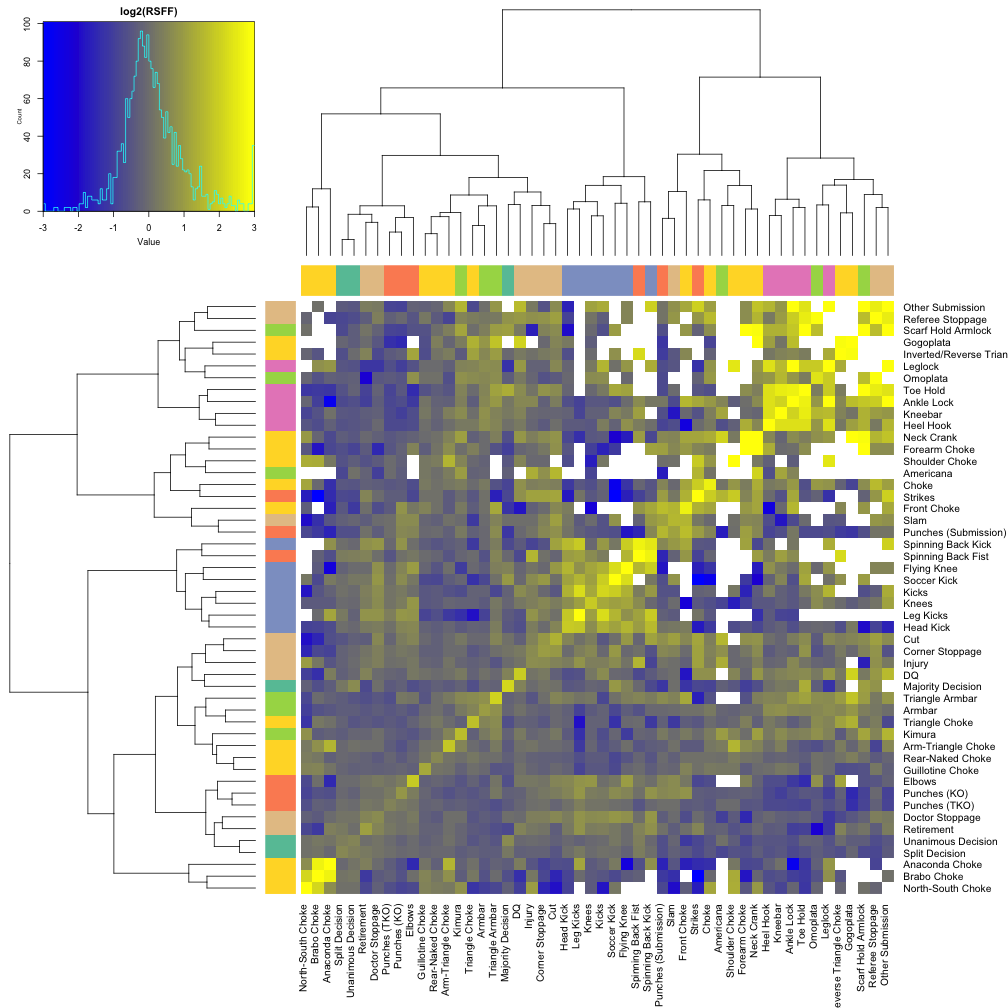
This heatmap shows that some sets of finishes are used by similar fighters. In particular, three groups of finishes emerge, each with sets of finishes that are used together:
- Chokes from front headlock: Brabo, Anaconda, North-South Choke
- Kicks: Head, Leg, Soccer, Flying, Spinning-Back Kick, Knees
- Leglocks: Heel Hook, Kneebar, Ankle Lock, Toehold
While there are clear groups that emerge as block-diagonal sets in the heatmap, it is less clear whether some of the other (primarily off-diagonal) linkages between finishes are real or whether they are only weak, chance associations. To determine which finishes reliably cooccur, I had to do some statistics.
Statistical analysis of finish cooccurrence
To determine if a pair of finishes cooccurs more (or less) frequently than expected, I needed to determine whether RSFF values like 1.5 are extreme or to be expected. A challenge with this is that an RSFF of 1.5 is likely less meaningful if the finishes are rare. If two finishes are rare, sometimes even a single instance of a fighter using two finishes yields a large RSFF. Thus, I needed to assess whether the value of RSFF for each finish-pair is extreme in light of the frequencies of these finishes. To do this, I used permutation analysis.
Permutation analysis is a powerful approach for investigating questions that use test-statistics with uncharacterized properties or with complicated dependencies that must be preserved. Using permutation analysis, we can break the dependence between pairs of finishes, which leads to elevated (or decreased) RSFF, while maintaining the overall frequency of individual finishes. Essentially, I will shuffle the finish records of all fighters while maintaining each fighter’s number of wins and the overall number of each finish across all fighters, and then calculate a null value of RSFF for each pair of finishes. This gives me one summary of RSFF values that could be expected if there were no dependent signals in the dataset. Generating many of these null datasets and values of RSFF provides a full null distribution of RSFF values for each finish pair. I then compared observed values of RSFF to the null distribution of RSFF to generate p-values. Because I carried out many comparisons I used a qvalue-based false discovery rate correction to determine which pairs of finishes were significant at an FDR of 0.05 (i.e. we expect that one out of twenty predictions is erroneous).
library(qvalue)
network_N_nullsamples <- 5000
RSFF_null <- function(results){
# randomized fighter finishes
results$Finish <- sample(results$Finish)
RSFF_calculate(results)
}
# generate null samples of RSFF
RSFF_null_samples <- parallel::mclapply(1:network_N_nullsamples, function(x){
RSFF_null(overall_results)
}, mc.cores = 7) %>%
bind_rows()
RSFF_null_summary <- RSFF_null_samples %>%
left_join(
RSFF_observed %>%
select(Finish_from, Finish_to, observed_RSFF = RSFF),
by = c("Finish_from", "Finish_to")) %>%
group_by(Finish_from, Finish_to) %>%
summarize(
p_observed = sum(observed_RSFF >= RSFF)/n(), # empirical p
null_lb = quantile(RSFF, probs = 0.025), # lower-bound on null RSFF
null_ub = quantile(RSFF, probs = 0.975) # upper-bound on null RSFF
) %>%
ungroup() %>%
# generate two-tailed p-value
mutate(p_observed = 1 - 2*abs(p_observed - 0.5)) %>%
mutate(p_observed = ifelse(p_observed == 0, 1/network_N_nullsamples, p_observed)) %>% # limit smallest p-value to 1/nperm
# generate q-values and significantly cooccuring finishes at an FDR of 0.05
mutate(q_observed = qvalue(.$p_observed, pi0.method="bootstrap")$qvalues) %>%
mutate(is_significantly_associated = ifelse(q_observed < 0.05, T, F))
# backjoin summary to RSFF_observed
RSFF_summary <- RSFF_observed %>%
select(Finish_from, Finish_to, Edge_count, RSFF) %>%
left_join(
RSFF_null_summary %>%
select(Finish_from, Finish_to, q_observed, is_significantly_associated),
by = c("Finish_from", "Finish_to"))A graphical network of MMA finishes
Now that I have determined which pairs of finishes fighters use together significantly more than expected, I can use this structure to better understand different styles of MMA fighters. I can take advantage of several pieces of information to do this:
- Having identified significant associations I only have to think about making sense of these significant associations, rather than worrying about all pairs of finishes.
- Stronger associations (more significant and higher RSFF) are likely more important since these pairs of finishes are used together the most.
- Positive cooccurrence is probably more useful than negative cooccurrence: if finish A is similar to finish B and C, it suggests that B is similar to C; while if A is dissimilar to B and C, we know very little about the relationship between B and C.
Across the 50 finishes, there are 289 pairs of finishes that significantly cooccur, among these, some associations are strong (high RSFF and low p/q-value) and others are weak. To visualize these cooccurrences, I used an undirected graphical network to organize finishes based on their cooccurrence effectively translating highly significant values of RSFF into closer proximity of finishes in a layout. To create this layout, I used the strongest connections in the network to guide the layout (so that some finishes that are weakly connected to many other finishes wouldn’t dominate the layout), and I used a spring-based, force-directed algorithm (Kamada-Kawai) to find an optimal layout.
# Visualize finish cooccurrence (RSFF) as a graph
suppressPackageStartupMessages(library(igraph))
suppressPackageStartupMessages(library(ggplot2))
library(ggraph)
finish_summary <- overall_results %>%
dplyr::ungroup() %>%
dplyr::count(Finish) %>%
left_join(general_finishes, by = "Finish")
edge_colors <- data.frame(RSFF = seq(from = -3, to = 3, length.out = 1000), color = green2red(1000))
## Prune edges based on:
# 1) >= 2 observed edges
# 2) statistically significant departure from randomness
# 3) cooccurrence more likely than chance
# 4) no self edges (e.g. armbar-armbar)
# removing low count edges and only looking at edges which are significantly associated
finish_relative_similarity_simple <- RSFF_summary %>%
mutate(log_RSFF = log2(RSFF)) %>%
filter(Edge_count >= 2,
is_significantly_associated,
log_RSFF > 0,
Finish_from != Finish_to) %>%
select(Finish_from, Finish_to, Edge_count, q_observed, log_RSFF) %>%
rowwise() %>%
mutate(color = edge_colors$color[which.min(abs(edge_colors$RSFF - log_RSFF))])
# rank edges based on both vertices
edge_pairs <- rbind(finish_relative_similarity_simple %>% rename(V_reference = Finish_from, V_target = Finish_to),
finish_relative_similarity_simple %>% rename(V_reference = Finish_to, V_target = Finish_from)) %>%
ungroup %>%
group_by(V_reference) %>%
arrange(q_observed, desc(log_RSFF)) %>%
mutate(Edge_rank = 1:n())
# prune edges based on edge ranks (minimum rank among both vertices)
finish_relative_similarity_simple <- finish_relative_similarity_simple %>%
mutate(Edge_rank = min(edge_pairs$Edge_rank[edge_pairs$V_reference %in% c(Finish_from, Finish_to) &
edge_pairs$V_target %in% c(Finish_from, Finish_to)])) %>%
# only use highly significant edges (breaking ties using effect size)
mutate(in_reduced_graph = ifelse(Edge_rank <= 3, T, F))
# Generate a network with saved edges and vertex information
finish_graph <- graph_from_data_frame(finish_relative_similarity_simple %>%
mutate(log_RSFF = pmax(pmin(log_RSFF, 3), -3)),
directed = F, vertices = finish_summary)
# layout nodes based on edges where "in_reduced_graph" is true
reduced_finish_graph=delete.edges(finish_graph, which(!(E(finish_graph)$in_reduced_graph)))
set.seed(13)
reduced_finish_graph <- createLayout(reduced_finish_graph, "igraph", algorithm = "kk")
# pass positions of nodes to main network
gg_graph <- createLayout(finish_graph, "manual", node.positions = data.frame(x = reduced_finish_graph$x, y = reduced_finish_graph$y))
graph_theme <- theme_minimal() +
theme(axis.text = element_blank(), panel.grid = element_blank(),
axis.title = element_blank(), legend.key.size = unit(0.25, "inches"),
legend.text = element_text(size = 18), legend.title = element_text(size = 25),
plot.background = element_rect(fill = "white", color = "white"), text = element_text(color = "black"),
legend.position = "bottom", legend.box = "horizontal", legend.title.align = 0.5)
color_scheme <- gg_graph %>%
select(General_Finish, color) %>%
unique() %>%
mutate(color = as.character(color),
General_Finish = as.character(General_Finish))
ggraph(data = gg_graph) +
geom_edge_link(aes(edge_width = -log2(q_observed)/12, colour = log_RSFF, edge_alpha = ifelse(in_reduced_graph, 0.75, 0.25))) +
geom_node_point(aes(size = log2(n)*1.2, color = General_Finish)) +
ggrepel::geom_label_repel(aes(label = name, x = x, y = y, fill = General_Finish), size = 7, color = "black", alpha = 0.5) +
scale_edge_colour_continuous(guide = "none", low = "gray75", high = "gray1", limits = c(0,3)) +
scale_edge_width_identity() +
scale_edge_alpha_identity(guide = "none") +
scale_color_manual("Finish category", values = color_scheme$color, limits = color_scheme$General_Finish, breaks = sort(color_scheme$General_Finish)) +
scale_fill_manual(guide = "none", values = color_scheme$color, limits = color_scheme$General_Finish, breaks = sort(color_scheme$General_Finish)) +
guides(colour = guide_legend(nrow = 2, title.position = "top", override.aes = list(size = 14))) +
scale_alpha_identity(guide = "none") +
scale_size_identity() +
graph_theme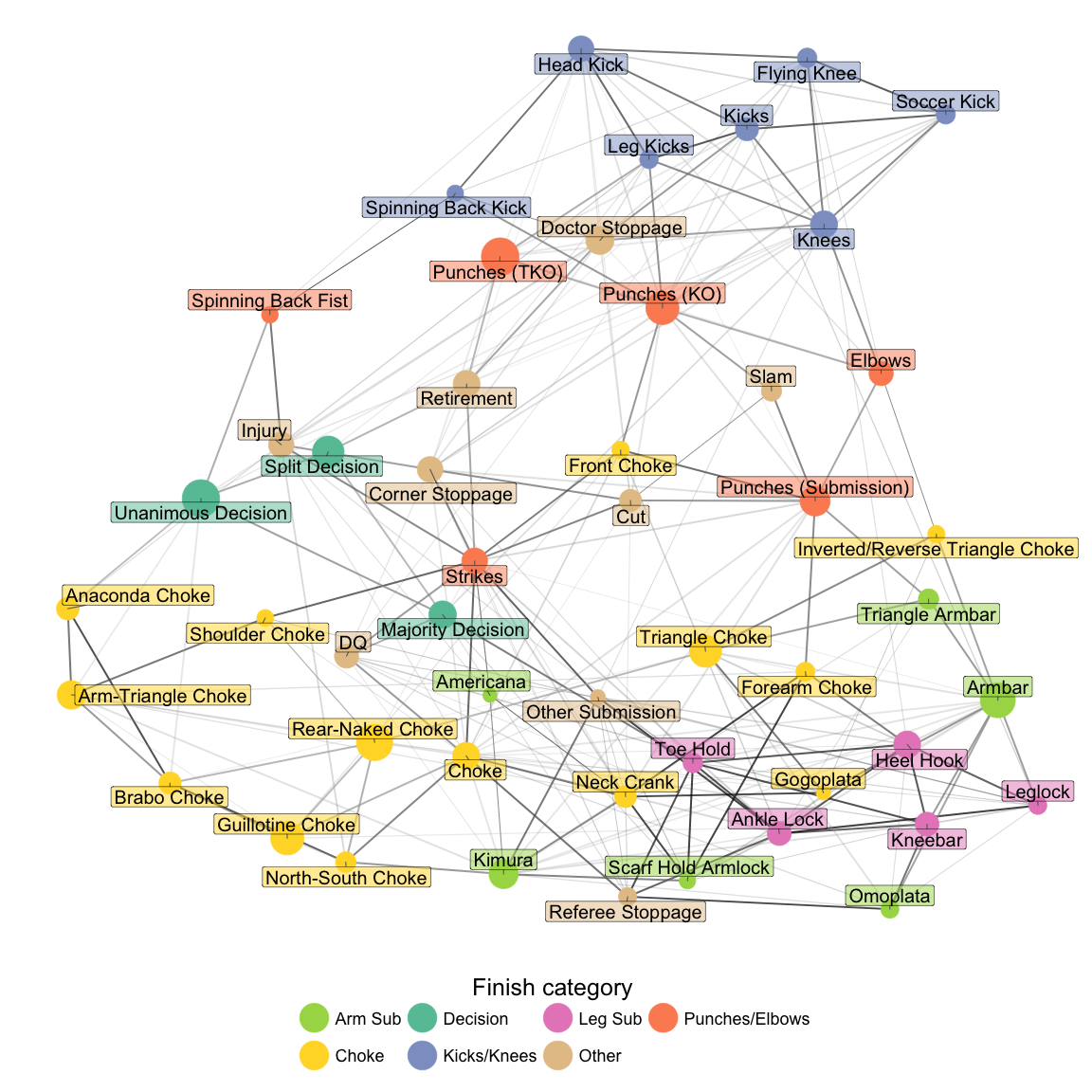
Overarching patterns in finishes
The heatmap analysis identified a few subsets of finishes used by fighters, but when viewed as a network of significantly cooccurring pairs of finishes, it is clear that relationships between finishes are far more nuanced. Finishes don’t resolve into isolated clusters; instead, they form a continuous network, with each finish coupled to stylistically similar finishes.
This finish network is almost linear, with some weak connections between each end of the line, such that the graph is bent into a “U.” The finishes at each end of the “U” are (1) kicks, elbows and knees, and (2) leg submissions and submissions from guard. Winning a TKO or KO by punches is associated with the kickboxing finishes, as would be expected; however, striking is also strongly associated with winning by decision, underscoring the importance of striking in winning by decision. In the bend of the “U” are chokes that require strong positional control: Arm-Triangle, Rear-Naked Choke, Anaconda, Darce and the North-South Choke. These chokes are also connected to winning by decision
Future Directions
I think this analysis is a good start to quantitatively defining MMA styles; but, I would also like to define the styles of fighters themselves. Because the vast majority of fighters have had a small number of fights, it would be easy to over-focus on finishes that a fighter has previously utilized. In my next post on MMA styles, I will discuss how such over-fitting can be avoided by balancing fighter-specific data with patterns across fighters using empirical Bayes.